Как подобрать подходящий критерий оценки прогноза для временных рядов

Оценка точности предсказаний при работе с временными данными предъявляет особые требования к выбору критериев. Правильное понимание того, какую метрику выбрать, способно существенно влиять на конечный результат анализа и последующие решения. Среди множества доступны различные методы, каждый из которых раскрывает модель с новой стороны и концентрируется на специфических ошибках. Метрика mae известна своей наглядностью и простотой в интерпретации, что делает её востребованным инструментом в ряде случаев.

Обзор основных типов показателей

Общее понятие о результатах прогноза даёт сравнение нескольких критериев, выделяющих разные аспекты ошибки. Важно учитывать, что даже небольшие различия в вычислениях отражают разные свойства и слабые места модели. Поэтому для комфортного и полного анализа стоит рассмотреть сразу несколько показателей. Они помогают обнаружить проблемы и выбрать курс для дальнейшей доработки.

Название	Описание	Особенности и применение
Среднеквадратическая ошибка (MSE)	Вычисляет среднее значение квадратов разностей между предсказанными и реальными данными. Используется для измерения совокупной величины ошибок.	Очень чувствительна к крупным отклонениям. Подходит там, где большие ошибки надо минимизировать, например в риск-ориентированных системах.
Квадратный корень из MSE (RMSE)	Возвращает показатель в тех же единицах, что и исходный ряд, что делает интерпретацию более понятной и практичной. Корень из среднего квадрата ошибки.	Наследует чувствительность MSE к выбросам, но позволяет видеть ошибку в тех же величинах, что данные, облегчая понимание для бизнес-аналитиков.
Средняя абсолютная ошибка (MAE)	Определяет среднее абсолютное расстояние между прогнозом и фактом. Не усиливает влияние больших ошибок так, как MSE.	Устойчивее к выбросам и шурам данных, даёт понятную оценку средней ошибки без чрезмерного акцента на единичных сильных отклонениях.
Средняя абсолютная процентная ошибка (MAPE)	Измеряет среднюю ошибку в процентах от фактических значений, помогая оценить относительное отклонение без учета абсолютных масштабов.	Полезна для оценки влияния ошибки в контексте бизнес-процессов и сравнения моделей на различных масштабах данных.

Как правильно интерпретировать метрики

Понимание характеристик каждого критерия нужно для того, чтобы не вводить себя в заблуждение по поводу качества модели. Если выбран показатель, чувствительный к аномалиям, несколько редких выбросов могут испортить все впечатление о системе. При этом другие инструменты могут показать более ровные и адекватные результаты. Следует учитывать специфику задачи, чтобы оценка соответствовала реальным ожиданиям.

Зависимость от типа ошибок

Показатели, применяющие квадратичное взвешивание ошибок, заставляют модель стремиться избегать крупных сбоев любой ценой. Это ведёт к повышенной осторожности и уменьшению риска серьезных потерь. Впрочем, подобные критерии могут ограничивать способность предсказывать экстремумы и резкие изменения.

Учет масштаба и интерпретируемость

Некоторые метрики дают значения, которые напрямую соотносятся с начальными величинами, что облегчает объяснение результатов не специалистам. Иные выражают ошибки в процентах, что хорошо подходит для оценки относительной эффективности и сравнения моделей на разных промежутках времени или инструментах.

Устойчивость к выбросам

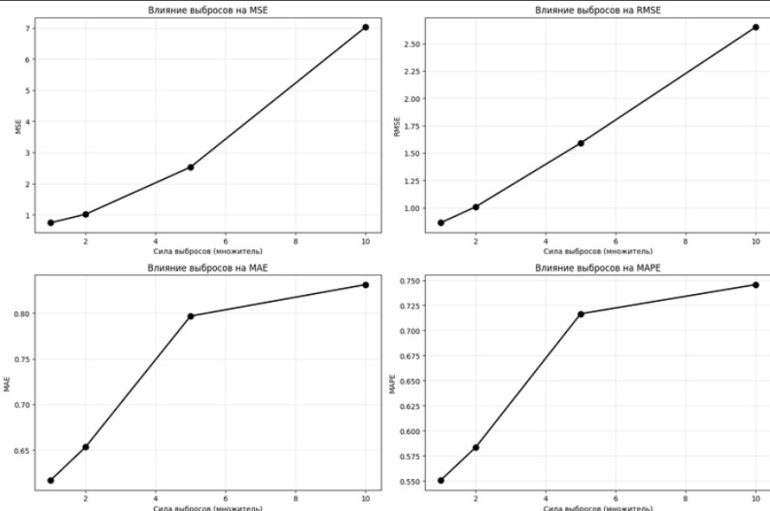
Когда временные ряды содержат аномальные значения, стоит отдавать предпочтение показателям, минимизирующим влияние таких выбросов. Это помогает сохранить объективную оценку и не переоценивать риски.

Влияние выбора оценочной формулы на качество прогноза

Использование одного критерия может не раскрыть всю сложность ошибки, тем более когда поведение данных существенно меняется с течением времени. Часто в работе применяют сразу несколько меток для выявления разнообразных сбоев. Такая комплексная оценка помогает взглянуть на модель шире и настроить её точнее.

Параметр оценки	Преимущества	Ограничения
MSE и RMSE	Чётко выделяют критичные ошибки, помогают избежать крупных промахов, улучшают надёжность модели в нестабильных условиях.	Могут переоценивать значимость единичных выбросов, что ведёт к чрезмерной консервативности и потере потенциала.
MAE	Показывает среднюю ошибку в удобной форме без излишнего влияния редких больших погрешностей.	Менее чувствителен к крупным аномалиям, что может скрывать потенциальные риски.
MAPE	Берёт в расчёт размер ошибки относительно фактических значений, что помогает понять экономический смысл прогноза.	Не всегда корректен при значениях рядом с нулём, может давать искажённые результаты в таких условиях.

Для эффективной оценки моделей и принятия решений в различных задачах целесообразно подходить к выбору с учётом как статистических особенностей данных, так и ключевых требований. Использование нескольких показателей позволит увидеть картину более полно и избежать скрытых проблем. В итоге, такой подход даст шанс построить наиболее точные и устоявшиеся прогнозы, открывая доступ к новым возможностям анализа.

Критерии качества прогноза не одинаково отражают разные типы ошибок и поведение модели. Применение соответствующих методов измерения нужно согласовывать с целями и характером временного ряда, чтобы получать максимально полезные результаты. Пробуя комбинировать несколько численных методов вместе и обращая внимание на отдельные нюансы, можно лучше понять слабые стороны построенных предсказаний. Метрики здесь становятся главными помощниками, открывающими весь спектр проблем и возможностей.